This blog post is an overview of some recent work, lead by my co-author Adam Yang (Yang et al., 2024), in which we tackle the issues of over-confidence in large language models and poor calibration, particularly when fine-tuned on small datasets or small collections of human feedback.
Taking a Bayesian approach, our method estimates the per-logit uncertainty over the next predicted token. This is particularly useful, for instance, for multiple choice question answering, classification tasks or reward modelling. We can also use our method to calculate the model evidence in order to tune model hyperparameters. Crucially, our method is applied as a post-hoc modification to a fine-tuned network 0: that is; can be applied following a similar workflow to existing post-training quantization methods such as AWQ (Lin et al., 2023) 0[0] , meaning that the standard, highly-optimised pre-training and fine-tuning pipelines can remain exactly the same, and the method can be applied to previously LoRA-finetuned models 1: or even fully fine-tuned models, although the computational cost of our method will be higher in this case 1[1] .
TL;DR:
- When fine-tuning an LLM, how do you know if your model has learned to perform the task well?
- Normally, the LLM only predicts the categorical parameters (logits)
- Our method additionally provides the variance (uncertainty) in these logit predictions (a Bayesian predictive distribution over the logits)
- the more fine-tuning data we see, the narrower the distribution, and the more certain our model is
- Most useful for single-token prediction tasks: reward modelling or multiple-choice question answering
- We can also calculate the model evidence to tune model hyperparameters
- Try it out with our library
(
pip install bayesian-lora)
Introduction
One notable property of large langauge models is that they have rather good calibration curves coming out of pre-training, and that the quality of the calibration swiftly deteriorates after fine-tuning 2: RLHF, or otherwise 2[2] . For instance, the GPT-4 technical report (OpenAI, 2023) 3: to be pedantic, this chart was produced in the full weight finetuning setting and not with LoRA adapters, yet the point still holds 3[3] illustrated this nicely with the following figure:
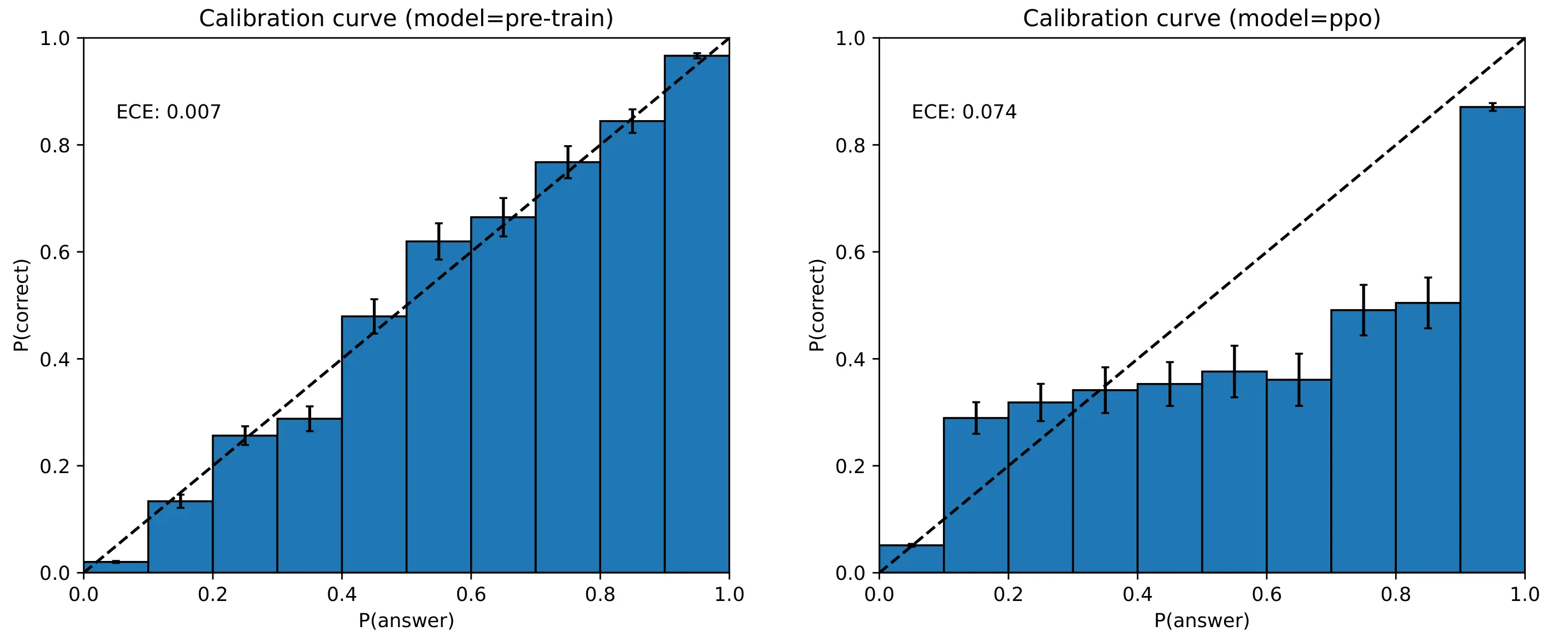
GPT-4 calibration curves for both the base pre-trained model and a PPO-finetuned model, evaluated on MMLU.
For those unfamiliar with calibration curves, we want the model to be confident
if its predictions are correct, and—perhaps most importantly—‘un-confident’
when its predictions are incorrect.
For instance, in a multiple choice task
4: we can predict classes in an
autoregressive language model with a single next-token prediction by merely
selecting the tokens corresponding to the class label (e.g. “ A”, “ B”, “ C” and so on) while disregarding all other tokens.
4[4]
if a model predicts some class “A” with 70% confidence, and it is a well
calibrated model, then in reality class “A” should be the correct answer about
70% of the time in the dataset. For a poorly calibrated model, we
would expect class “A” to be correct \(p \ne 70\)% of the time. Ideally, our
models would have \(\P(\mathrm{answer}) = \P(\mathrm{correct})\) everywhere.
Our method provides a Bayesian predictive distribution over the model’s logits. Where a model might have previously placed 90% of its confidence behind a single logit, our method provides us with a predictive distribution over this logit’s value 5: at risk of being ambiguous, our method isn’t constrained to single-logit predictions; we can predict the distribution over a single logit, a subset of logits, or all the logits 5[5] ; allowing us to examine the variance hence the level of uncertainty 6: that is, the uncertainty due to lack of data / test distribution shift; influenced by the chosen prior 6[6] in this prediction which appears confident if we only look at the point estimates of the logits.
Why Fine-Tuning?
There has been some previous interest in bringing Bayesian inference to LLMs, however most of this work has focused on the pre-training setting (Xue et al., 2021; Cinquin et al., 2021; Chen et al., 2022). As some of these works themselves conclude, there is little to be gained from a Bayesian treatment of the pre-training setting; where the abundance of data—the trillions of tokens—drives uncertainty low for in-distribution test points, the models are surprisingly well calibrated (Kadavath et al., 2022) and the additional cost of the Bayesian machinery becomes exorbitant.
In contrast, the advantages of Bayes become more apparent in the fine-tuning setting, where the smaller datasets tend to yield poor calibration (OpenAI, 2023). Further, the popularity of LoRA adapters (Hu et al., 2022) for model fine-tuning provides a significant reduction in the number of parameters we need to consider, which goes some way towards making the usually expensive Bayesian methods applicable to language models. Our method—described below—is based on a Laplace approximation, with a Kronecker-factored approximation to the Fisher (MacKay, 1992; Daxberger et al., 2022). In addition, the alternating wide-then-narrow shapes of LoRA adapters' layers affords our method a particularly efficient low-rank approximation to the Kronecker-factored approximate curvature (Eschenhagen et al., 2023), further reducing the memory cost of (approximate) Bayesian inference in the LLM .
Hence, our method can be applied to fine-tuned models, to estimate the uncertainty in each token’s prediction. While we focus on LoRA fine-tuning, this isn’t necessary beyond reducing the memory cost, and our method can be applied to full fine-tuning too.
Laplace LoRA Method
What follows is a short overview of our method, which we call Laplace LoRA—for the full details, refer to the paper.
Parameter-Efficient Fine-Tuning
As set out in the introduction, we consider parameter-efficient fine-tuning of LLMs using low-rank adapters (Hu et al., 2022). For any given weight matrix \(\rmW \in \R^{m \times n}\), mapping \(n\)-dimensional inputs to \(m\)-dimensional outputs, a LoRA adapter is just a low-rank weight perturbation \(\Delta\rmW = \rmB\rmA\), parametrised by \(\rmB \in \R^{m \times r}\) and \(\rmA \in \R^{r \times n}\), which, when added to \(\rmW\), alters the behaviour of that layer.
Letting \(\rva \in \R^{n}\) be the input activation to the layer, and \(\rvs \in \R^{m}\) the pre-activations, the forward pass becomes:
\[\begin{equation} \label{eq:lora} \rvs = (\rmW + \Delta\rmW)\rva = (\rmW + \rmB\rmA)\rva = \rmW\rva + \rmB\rmA\rva. \end{equation} \]
We usually set rank \(r\) of this adapter to some \(r \ll \min(m, n)\) to get a low-rank adapter. Visually,

In transformers, typically \(m = n \approx 4096\), and we often select fairly low ranks such as \(r \approx 8\). During normal training or fine-tuning, the number of parameters in this linear layer is \(mn\) (e.g. 16.7 million) while in LoRA fine-tuning, we freeze \(\rmW\) and only have \(rn + rm\) (e.g. 65 thousand) trainable parameters as a result—a significant reduction which makes a Bayesian treatment of these parameters feasible.
Laplace Approximations
So far, everything has resembled standard fine-tuning. We are now interested in finding a distribution over the fine-tuned weights, such that we can calculate the model evidence or the predictive distributions. For this, we use a Laplace approximation, which represents the weight posterior as a Gaussian, centred at the maximum a-posteriori weights, and with covariance equal to the Fisher information matrix.
Posterior Approximation
Let \(\vtheta\) denote all the trainable 7: that is, distinct from all the weights in the LLM, which may exclude frozen and quantized pre-trained model weights 7[7] weights of our network. We’ll also use \(\rmX \in \gV^{B \times N}\) to denote the inputs to the LLM, with \(\gV\) the vocabulary set 8: or set of possible tokens 8[8] , \(B\) the batch size, and \(N\) the (maximum; i.e. left-padded) sequence length. The targets are \(\rvy\in\gY^{B}\), where \(\gY\) could differ from \(\gV\) (e.g. multiple choice question answering, sentiment classification) or it could be the same as \(\gV\) (e.g. next token prediction, autoregressive decoding).
For models trained with a cross-entropy loss, the likelihood \(\P(\rvy \vert \rmX, \vtheta)\) is just a Categorical distribution, with logits given by the network prediction \(f_{\vtheta}(\rmX)\).
For the prior distribution over the fine-tuning weights, we simply use an isotropic Gaussian prior with precision \(\lambda\):
\[\begin{equation} \label{eq:lora_prior} \P(\vtheta) = \gN(\mathbf{0}, \lambda^{-1}\rmI). \end{equation} \]
Note that a normal training run (i.e. minimising a cross entropy loss with weight decay) is equivalent to maximising a log joint, \(\log \P(\rvy, \rmX, \vtheta)\) with this likelihood and prior. That is, it is equivalent to maximising the following:
\[\begin{align} \log\P(\gD, \vtheta) &= \log \P(\rvy \vert \rmX, \vtheta) + \log \P(\vtheta) \label{eq:log_joint} \\ &= \log \P(\rvy \vert \rmX, \vtheta) + \log \gN(\vtheta; \mathbf{0}, \lambda\rmI) \\ &= \log \P(\rvy \vert \rmX, \vtheta) + \frac{\lambda}{2}\Vert \vtheta \Vert_{2}^{2} + \mathrm{const}. \\ &\doteq \gL(\rvy, \rmX; \vtheta). \end{align} \]
We can see that the effect of the prior in Equation \(\ref{eq:lora_prior}\) is the same as regularising the L2 norm of the weights; in other words, applying weight decay with a strength of \(\lambda / 2\). Hence, we can re-use the weights from any previous training run with sensible weight decay (e.g. optimised with AdamW, where the default weight decay is \(0.01\)).
Since we’re after the posterior distribution over the weights after fine-tuning, we need to calculate:
\[\label{eq:llm_weight_posterior} \begin{equation} \P(\vtheta \vert \rmX, \rvy) = \frac{\P(\rvy \vert \rmX, \vtheta) \P(\vtheta)}{p(\rmX, \rvy)}. \end{equation} \]
The marginal likelihood in the denominator is usually intractable, so we turn to one of the many approximations in the Bayesian’s toolbox; in this case the Laplace approximation (MacKay, 1992; Daxberger et al., 2022). We start with the regularised training solution (i.e. maximising \(\gL(\rvy, \rmX; \vtheta)\)), which we will refer to as the maximum a-posteriori solution (\(\vtheta_{\mathrm{MAP}}\)) henceforth:
\[\begin{align} \gL(\rvy, \rmX; \vtheta) &= \log \P(\rvy \vert \rmX, \vtheta) + \log \P(\vtheta) = \log \P(\vtheta \vert \rmX, \rvy) + \mathrm{const}. \\ \vtheta_{\mathrm{MAP}} &= \argmax_{\vtheta}\gL(\rvy, \rmX; \vtheta). \end{align} \]
Now, taking a second-order Taylor expansion of the log-joint around \(\vtheta_{\mathrm{MAP}}\), we get
\[\begin{equation} \label{eq:log_joint_taylor} \gL(\rvy, \rmX; \vtheta) \approx \gL(\rvy, \rmX; \vtheta_{\mathrm{MAP}}) - \frac{1}{2}(\vtheta - \vtheta_{\mathrm{MAP}})^{\top}\big(-\nabla_{\vtheta}^{2}\gL(\rvy, \rmX; \vtheta)\vert_{\vtheta_{\mathrm{MAP}}}\big)(\vtheta - \vtheta_{\mathrm{MAP}}). \end{equation} \]
Notice that the first-order term in Equation \(\ref{eq:log_joint_taylor}\) disappears, on account of the gradient of the log-joint being \(0\) at the MAP parameter location 9: That is, we’d expect the gradient of the MAP objective, evaluated at the MAP parameter location, to be (approximately) zero after training. 9[9] , and we have written the second-order term in negated form by negating the Hessian inside the brackets 10: This is just to make matching terms more explicit later. 10[10] .
Now, matching terms with the quadratic forms in Equations \(\ref{eq:log_joint_taylor}\) and a log Gaussian density, we arrive at the Laplace approximation of the unnormalised posterior \(\P(\vtheta \vert \rmX, \rvy)\) as a Gaussian centred at \(\vtheta_{\mathrm{MAP}}\) with precision \(\mLambda_{\mathrm{post}}\):
\[\begin{align} \P(\vtheta \vert \rmX, \rvy) &\approx \gN(\vtheta; \vtheta_{\mathrm{MAP}}, \mSigma_{\mathrm{post}}) \\ \mSigma_{\mathrm{post}} &= \mLambda_{\mathrm{post}}^{-1} \\ \mLambda_{\mathrm{post}} &= -\nabla_{\vtheta}^{2}\gL(\rvy, \rmX; \vtheta)\vert_{\vtheta_{\mathrm{MAP}}} \\ &= -\nabla^{2}_{\vtheta}\log \P(\rvy \vert \rmX; \vtheta)\vert_{\vtheta_{\mathrm{MAP}}} - \nabla^{2}_{\vtheta}\log \gN(\vtheta; \mathbf{0}, \lambda^{-1}\rmI)\vert_{\vtheta_{\mathrm{MAP}}} \\ &= -\nabla^{2}_{\vtheta}\log \P(\rvy \vert \rmX; \vtheta)\vert_{\vtheta_{\mathrm{MAP}}} + \lambda\rmI \label{eq:sigma_post_terms}. \end{align} \]
There are however two issues with \(\mLambda_{\mathrm{post}}\). The first is that we need it to be positive definite; looking at the first term in Equation \(\ref{eq:sigma_post_terms}\), we see that this is the case if the likelihood is convex at \(\vtheta_{\mathrm{MAP}}\), and of course the outputs \(\rvy\) are within the support of the likelihood 11: i.e. \(\P(\rvy \vert \rmX; \vtheta) > 0\), where the inequality is strict 11[11] . However with complicated neural network likelihoods, this local convexity condition is not guaranteed to hold. The second issue with \(\mLambda_{\mathrm{post}}\) is that it is a very large \(P \times P\) matrix, where \(P\) is the number of elements in \(\vtheta\), making it impractical to work with directly.
Fisher Information
To resolve the first of these issues, we instead use the Fisher information matrix instead of the Hessian directly. The Fisher is defined 12: do see my previous article on second order methods to gain some intuition about this quantity. 12[12] as:
\[\begin{equation} \label{eq:fim} \rmF(\vtheta) \doteq \E_{\substack{\hat{\rvx} \sim \gD \\ \hat{\ervy} \sim \P(\rvy \vert f_{\vtheta}(\hat{\rvx}))}}\left[\nabla_{\vtheta}\P(\hat{\ervy} \vert f_{\vtheta}(\hat{\rvx}))\big(\nabla_{\vtheta}\P(\hat{\ervy} \vert f_{\vtheta}(\hat{\rvx}))\big)^{\top}\right], \end{equation} \]
where we use \(\hat{\ervy} \sim \P(\rvy \vert f_{\vtheta}(\hat{\rvx}))\) to denote samples drawn from the model’s output distribution. This is now a positive semi-definite matrix, which resolves the first of our two issues.
Kronecker-Factored Approximate Curvature
To reduce the memory requirements, we use a low-rank Kronecker-factored approximation to the curvature. This involves three approximations:
1. We first treat the Fisher information as a block-diagonal matrix (i.e. treating each of the network’s layers \(L1, L2, \ldots\) independentally)

2. Following the standard K-FAC procedure (Martens et al., 2015), we further factorise each of these blocks \(\rmF_{\ell\ell}\) as a Kronecker product of two smaller matrices, \(\rmA_{\ell-1}\) and \(\rmS_{\ell}\). These correspond to the expected outer product of layer \(\ell\)’s input activations \(\rva_{\ell-1}\) and output gradients \(\gD\rvs_{\ell} \doteq \nabla_{\rvs_{\ell}}\log \P(\rvy \vert \rmX; \vtheta)\), respectively, where \(\rvs_{\ell}\) is the pre-activation output of layer \(\ell\). That is,
\[\begin{equation} \label{eq:kfac} \rmF_{\ell\ell} \approx \underbrace{\E\left[\rva_{\ell-1}\rva_{\ell-1}^{\top}\right]}_{\rmA_{\ell-1}} \otimes \underbrace{\E\left[\gD\rvs_{\ell}\gD\rvs_{\ell}^{\top}\right]}_{\rmS_{\ell}}, \end{equation} \]
where the expectations are as in Equation \(\ref{eq:fim}\). Note that this second approximation comes not from the Kronecker factorisation, but the independent expectations.
3. Despite \(\rmA_{\ell-1}\) and \(\rmS_{\ell}\) being smaller than \(\rmF_{\ell\ell}\), the first factor scales as the square of the layer’s input width, while the second factor scales as the square of the layer’s output width.
Since we are working with LoRA adapters, layers \(\ell\) alternate between wide-input-narrow-output and vice versa; hence one of the two Kronecker factors will be very large (e.g. \(4096 \times 4096\)), while the other will be very small (e.g. \(8 \times 8\)).
To this end, we use an incremental 13: that is, to avoid having to materialise the full matrix and run a big SVD, we incrementally compute the SVD as we iterate over batches 13[13] SVD to estimate the larger of these factors as a product of two new low-rank factors. For example if \(\rmA_{\ell-1} \in \R^{d \times d}\) is the larger factor, we approximate it as \(\rmA_{\ell-1} \approx \rmB\rmB^{\top}\) for some \(\rmB^{d\times n_{\mathrm{kfac}}}\); thus saving memory.
Linearized Prediction
All the above was to get a tractable way of obtaining the paramters of our Gaussian approximate posterior. Recall, that the posterior is a Gaussian \(\P(\vtheta \vert \rmX, \rvy) \approx \gN(\vtheta; \vtheta_{\mathrm{MAP}}, \mSigma_{\mathrm{post}})\), centred at the MAP parameter locations (e.g. from a previous training run), with a block-diagonal covariance matrix given by the inverse of our low-rank K-FAC scheme (plus the diagonal prior term).
We can now use this posterior to make predictions. The Laplace approximation has strong connections to linearising the network (Antorán et al., 2022), and it is often found that predicting from a linearised model is more effective than doing the intuitive thing of sampling a set of weights from the posterior and using those to predict using the full network. That is, for some test input \(\rvx_{\star}\), the linearised network is
\[\begin{equation} \label{eq:linearised_net} f_{\vtheta}(\rvx_{\star}) \approx f_{\vtheta_{\mathrm{MAP}}}(\rvx_{\star}) + \nabla_{\vtheta}f_{\vtheta}(\rvx_{\star})\vert^{\top}_{\vtheta_{\mathrm{MAP}}}(\vtheta - \vtheta_{\mathrm{MAP}}). \end{equation} \]
This is now just a linear transformation of the Gaussian-distributed weights, hence we can easily integrate these out 14: see my previous article on Gaussians for more on this 14[14] to get a Gaussian predictive distribution on the output logits:
\[\begin{equation} \label{eq:posterior_predictive} f_{\vtheta}(\rvx_{\star}) \sim \gN\big(\rvy; f_{\vtheta_{\mathrm{MAP}}}(\rvx_{\star}), \mLambda\big), \end{equation} \]
for
\[\begin{equation} \label{eq:post_pred_cov} \mLambda = \big(\nabla_{\vtheta}f_{\vtheta}(\rvx_{\star})\vert^{\top}_{\vtheta_{\mathrm{MAP}}}\big)\mSigma_{\mathrm{post}}\big(\nabla_{\vtheta}f_{\vtheta}(\rvx_{\star})\vert_{\vtheta_{\mathrm{MAP}}}\big). \end{equation} \]
Decomposing the above using a Cholesky decomposition, \(\mLambda = \rmL\rmL^{\top}\), we can draw posterior samples using reparametrised sampling:
\[\begin{equation} \label{eq:reparam_sampling} \hat{\rvy} = f_{\vtheta}(\rvx_{\star}) = f_{\vtheta_{\mathrm{MAP}}}(\rvx_{\star}) + \rmL\vxi, \hskip{2em}\vxi \sim \gN(\mathbf{0}, \rmI). \end{equation} \]
Marginal Likelihood
Finally, we can also use the marginal likelihood (or model evidence), which we have in closed form owing to our Laplace approximation, to optimise hyperparameters such as our selected prior precision. The marginal likelihood can be approximated in closed form as
\[\begin{align*} \P(\rvy \vert \rmX) &= \int \P(\rvy \vert \rmX; \vtheta)\P(\vtheta) d\vtheta \\ &\approx \exp\big(\gL(\rvy, \rmX; \vtheta_{\mathrm{MAP}})\big)(2\pi)^{D/2}\det(\mSigma_{\mathrm{post}})^{1/2}. \end{align*} \]
This quantity can be used as an objective to tune the value of \(\lambda\) for instance.
Using this Method
Do look at the accompanying repository and the documentation for code examples.